В математике различные типы чисел изучаются с самого своего зарождения. Существует большое количество множеств и подмножеств чисел. Среди них выделяют целые числа, рациональные, иррациональные, натуральные, четные, нечетные, комплексные и дробные. Сегодня разберем информацию о последнем множестве - дробных числах.
Определение дробей
Дроби - это числа, состоящие из целой части и долей единицы. Также, как и целых чисел, существует бесконечное множество дробных, между двумя целыми. В математике действия с дробями выполняются, так как с целыми и натуральными числами. Это довольно просто и научиться этому можно за пару занятий.
В статье представлено два вида
Обыкновенные дроби
Обыкновенные дроби представляют собой целую часть a и два числа записанных через дробную черту b/c. Обыкновенные дроби могут быть крайне удобны, если дробную часть нельзя представить в рациональном десятичном виде. Кроме того, арифметические операции удобнее производить через дробную черту. Верхняя часть называется числитель, нижняя - знаменатель.
Действия с обыкновенными дробями: примеры
Основное свойство дроби. При умножении числителя и знаменателя на одно и то же число, не являющееся нулем, в результате получается число равное данному. Это свойство дроби отлично помогает привести знаменатель для сложения (об этом будет рассказано ниже) или сократить дробь, сделать ее удобнее для счета. a/b = a*c/b*c. К примеру, 36/24 = 6/4 или 9/13 = 18/26
Приведение к общему знаменателю. Чтобы привести знаменатель дроби необходимо представить знаменатель в виде множителей, а затем помножить на недостающие числа. Например, 7/15 и 12/30; 7/5*3 и 12/5*3*2. Видим, что знаменатели отличаются двойкой, поэтому умножаем числитель и знаменатель первой дроби на 2. Получаем: 14/30 и 12/30.
Составные дроби - обыкновенные дроби с выделенной целой частью. (A b/c) Чтобы представить составную дробь в виде обыкновенной, необходимо умножить число, стоящее перед дробью на знаменатель, а затем сложить с числителем: (A*c + b)/c.
Арифметические действия с дробями
Не лишним будет рассмотреть известные арифметические действия только при работе с дробными числами.
Сложение и вычитание. Складывать и вычитать обыкновенные дроби точно так же легко, как и целые числа, за исключением одной трудности - наличия дробной черты. Складывая дроби с одинаковым знаменателем, необходимо сложить лишь числители обеих дробей, знаменатели остаются без изменения. Например: 5/7 + 1/7 = (5+1)/7 = 6/7
Если же знаменатели двух дробей представляют собой разные числа сначала нужно привести их к общему (как это сделать было рассмотрено выше). 1/8 + 3/2 = 1/2*2*2 + 3/2 = 1/8 + 3*4/2*4 = 1/8 + 12/8 = 13/8. Вычитание происходит по точно такому же принципу: 8/9 - 2/3 = 8/9 - 6/9 = 2/9.
Умножение и деление. Действия с дробями по умножению происходят по следующему принципу: отдельно перемножаются числители и знаменатели. В общем виде формула умножения выглядит так: a/b *c/d = a*c/b*d. Кроме того, по мере умножения можно сократить дробь, исключая одинаковые множители из числителя и знаменателя. Выражаясь другим языком, числитель и знаменатель делится на одно и то же число: 4/16 = 4/4*4 = 1/4.
Для деления одной обыкновенной дроби на другую, нужно поменять числитель и знаменатель делителя и выполнить умножение двух дробей, по принципу, рассмотренному ранее: 5/11: 25/11 = 5/11 * 11/25 = 5*11/11*25 = 1/5
Десятичные дроби
Десятичные дроби являются более популярной и часто используемой версией дробных чисел. Их проще записать в строчку или представить на компьютере. Структура десятичной дроби такая: сначала записывается целое число, а затем, после запятой, записывается дробная часть. По своей сути десятичные дроби - это составные обыкновенные дроби, однако их дробная часть представлена числом, деленным на кратное цифре 10. Отсюда и произошло их название. Действия с дробями десятичными аналогичны действиям с целыми числами, так как они так же записаны в десятичной системе счисления. Также в отличие от обыкновенных дробей, десятичные могут быть иррациональными. Это значит, что они могут быть бесконечны. Записываются они так 7,(3). Читается такая запись: семь целых, три десятых в периоде.
Основные действия с десятичными числами
Сложение и вычитание десятичных дробей. Выполнить действия с дробями не сложнее, чем с целыми натуральными числами. Правила абсолютно аналогичны с теми, что используют при сложении или вычитании натуральных чисел. Их точно так же можно считать столбиком, однако при необходимости заменять недостающие места нулями. Например: 5,5697 - 1,12. Для того чтобы выполнить вычитание столбиком нужно уравнять количество чисел после запятой: (5,5697 - 1,1200). Так, числовое значение не измениться и можно будет считать в столбик.
Действия с десятичными дробями нельзя производить, если одно из них имеет иррациональный вид. Для этого нужно перевести оба числа в обыкновенные дроби, а затем пользоваться приемами, описанными ранее.
Умножение и деление. Умножение десятичных дробей аналогично умножению натуральных. Их также можно умножать столбиком, просто, не обращая внимания на запятую, а затем отделить запятой в итоговом значении такое же количество знаков, сколько в сумме после запятой было в двух десятичных дробях. К примеру, 1,5 * 2,23 = 3,345. Все очень просто, и не должно вызвать затруднений, если вы уже овладели умножением натуральных чисел.
Деление также совпадает с делением натуральных чисел, но с небольшим отступлением. Чтобы разделить на десятичное число столбиком необходимо отбросить запятую в делителе, и умножить делимое на число знаков, стоявших после запятой в делителе. После чего выполнять деление как с натуральными числами. При неполном делении можно добавлять нули к делимому справа, также прибавляя ноль в ответ после запятой.
Примеры действий с десятичными дробями. Десятичные дроби - очень удобный инструмент для арифметического счета. Они сочетают в себе удобство натуральных, целых чисел и точность обыкновенных дробей. К тому же довольно просто перевести одни дроби в другие. Действия с дробями не отличаются от действий с натуральными числами.
- Сложение: 1,5 + 2,7 = 4,2
- Вычитание: 3,1 - 1,6 = 1,5
- Умножение: 1,7 * 2,3 = 3,91
- Деление: 3,6: 0,6 = 6
Кроме того, десятичные дроби подходят для представления процентов. Так, 100 % = 1; 60 % = 0,6; и наоборот: 0,659 = 65,9 %.
Вот и все, что нужно знать о дробях. В статье было рассмотрено два вида дробей - обыкновенные и десятичные. Оба довольно простые в вычислении, и если вы полностью овладели натуральными числами и действиями с ними, можете смело приступать к изучению дробных.
Расширение дроби. Сокращение дроби. Сравнение дробей.
Приведение к общему знаменателю. Сложение и вычитание дробей.
Умножение дробей. Деление дробей.
Расширение дроби. Значение дроби не меняется, если умножить её числитель и знаменатель на одно и то же число, отличное от нуля расширением дроби . Например,
Сокращение дроби.
Значение дроби не меняется,
если разделить её числитель
и
знаменатель на одно и то же число, отличное от нуля
.
Это преобразование называется сокращением дроби
. Например,
Сравнение дробей. Из двух дробей с одинаковыми числителями та больше, знаменатель которой меньше:
Из двух дробей с одинаковыми знаменателями та больше, числитель которой больше:
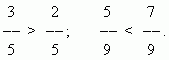
Для сравнения дробей, у которых числители и знаменатели различны, необходимо расширить их, чтобы привести к общему знаменателю.
П р и м е р. Сравнить две дроби:
Использованное здесь преобразование называется приведением дробей к общему знаменателю .
Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того, чтобы сложить дроби, надо сложить их числители, а для того, чтобы вычесть дроби, надо вычесть их числители (в том же порядке). Полученная сумма или разность будет числителем результата; знаменатель останется тем же. Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел мы рекомендуем сначала преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется, к виду смешанного числа.
П р и м е р .
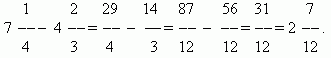
Умножение дробей. Умножить некоторое число на дробь означает умножить его на числитель и разделить произведение на знаменатель. Следовательно, мы имеем общее правило умножения дробей: для перемножения дробей необходимо перемножить отдельно их числители и знаменатели и разделить первое произведение на второе .
Дроби бывают обыкновенные и десятичные. Когда школьник узнает о существовании последних, он начинает при каждом удобном случае переводить все, что возможно, в десятичный вид, даже если этого не требуется.
Как ни странно, у старшеклассников и студентов предпочтения меняются, потому что проще выполнять многие арифметические действия с обыкновенными дробями. Да и значения, с которыми имеют дело выпускники, преобразовать в десятичный вид без потерь порой бывает попросту невозможно. В результате оба вида дробей оказываются, так или иначе, приспособлены к делу и обладают своими преимуществами и недостатками. Посмотрим, как с ними работать.
Определение
Дроби - это те же доли. Если в апельсине десять долек, а вам дали одну, то у вас в руке 1/10 часть фрукта. При такой записи, как в предыдущем предложении, дробь будет называться обыкновенной. Если написать то же самое как 0,1 - десятичной. Оба варианта являются равноправными, однако имеют свои преимущества. Первый вариант удобнее при умножении и делении, второй - при сложении, вычитании и в ряде других случаев.
Как перевести дробь в другой вид
Предположим, у вас есть обыкновенная дробь, и вы хотите сделать из неё десятичную. Что для этого нужно сделать?
К слову сказать, нужно заранее определиться, что не любое число можно без проблем записать в десятичном виде. Иногда приходится результат округлять, теряя некоторое количество знаков после запятой, а во многих областях - например, в точных науках - это совершено непозволительная роскошь. В то же время действия с десятичными и обыкновенными дробями в 5 классе позволяют осуществлять такой перевод из одного вида в другой без помех, хотя бы в качестве тренировки.
Если из знаменателя путём умножения или деления на целое число можно получить значение, кратное 10, перевод пройдёт без каких-либо трудностей: ¾ превращается в 0,75, 13/20 - в 0,65.
Обратная процедура выполняется ещё проще, поскольку из десятичной дроби можно всегда получить обыкновенную без потерь в точности. Например, 0,2 становится 1/5, а 0,08 - 4/25.
Внутренние преобразования
Прежде чем осуществлять совместные действия с обыкновенными дробями, нужно подготовить числа к возможным математическим операциям.
Перво-наперво нужно привести все имеющиеся в примере дроби к одному общему виду. Они должны быть либо обыкновенными, либо десятичными. Сразу оговоримся, что умножение и деление удобнее выполнять с первыми.
В подготовке чисел к дальнейшим действиям вам поможет правило, известное как и используемое как в первые годы изучения предмета, так и в высшей математике, которую изучают в университетах.
Свойства дробей
Предположим, у вас есть некоторое значение. Скажем, 2/3. Что изменится, если вы умножите числитель и знаменатель на 3? Получится 6/9. А если на миллион? 2000000/3000000. Но постойте, ведь число качественно совершенно не меняется - 2/3 остаются равны 2000000/3000000. Меняется только форма, но не содержание. То же самое произойдёт при делении обеих частей на одно и то же значение. В этом и заключается основное свойство дроби, которое неоднократно поможет вам производить действия с десятичными и обыкновенными дробями на контрольных и экзаменах.
Умножение числителя и знаменателя на одно и то же число называется расширением дроби, а деление - сокращением. Надо сказать, что зачеркивание одинаковых чисел в верхней и нижней части при перемножении и делении дробей - удивительно приятная процедура (в рамках урока математики, конечно). Создается впечатление, что ответ уже близок и пример практически решен.
Неправильные дроби
Неправильной дробью называется такая, у которой числитель больше или равен знаменателю. Иными словами, если у неё можно выделить целую часть, она попадает под это определение.
Если такое число (большее либо равное единице) представлено в виде обыкновенной дроби, она будет называться неправильной. А если числитель меньше знаменателя - правильной. Оба вида одинаково удобны при осуществлении возможных действий с обыкновенными дробями. Их можно беспрепятственно умножать и делить, складывать и вычитать.
Если же одновременно выделена целая часть и при этом имеется остаток в виде дроби, полученное число будет называться смешанным. В будущем вы столкнетесь с различными способами комбинации таких структур с переменными, а также решением уравнений, где потребуются эти знания.
Арифметические операции
Если с основным свойством дроби всё ясно, то как вести себя при перемножении дробей? Действия с обыкновенными дробями в 5 классе подразумевают все виды арифметических операций, которые выполняются двумя различными способами.
Умножение и деление выполняются очень просто. В первом случае просто перемножаются числители и знаменатели двух дробей. Во втором - то же самое, только крест-накрест. Таким образом, числитель первой дроби умножается на знаменатель второй, и наоборот.
Для выполнения сложения и вычитания нужно произвести дополнительное действие - привести все компоненты выражения к общему знаменателю. Это значит, что нижние части дробей должны быть изменены до одинакового значения - числа, кратного обоим имеющимся знаменателям. Например, для 2 и 5 это будет 10. Для 3 и 6 - 6. Но что тогда делать с верхней частью? Мы же не можем оставить её в прежнем виде, если изменили нижнюю. Согласно основному свойству дроби мы умножим числитель на то же число, что и знаменатель. Эта операция должна быть произведена с каждым из чисел, которые мы будем складывать или вычитать. Впрочем, такие действия с обыкновенными дробями в 6 классе выполняются уже «на автомате», а трудности возникают только на начальном этапе изучения темы.
Сравнение
Если у двух дробей одинаковый знаменатель, то больше будет та из них, числитель которой больше. Если же одинаковы верхние части, то больше будет та, у которой меньше знаменатель. Стоит иметь в виду, что столь удачные ситуации для сравнения выпадают нечасто. Скорее всего, и верхние, и нижние части выражений совпадать не будут. Тогда понадобится вспомнить про возможные действия с обыкновенными дробями и использовать приём, применяемый при сложении и вычитании. Кроме того, помните, что если мы говорим об отрицательных числах, то большая по модулю дробь окажется меньшей.
Преимущества обыкновенных дробей
Случается, что преподаватели говорят детям одну фразу, содержание которой можно выразить так: чем больше информации дано при формулировке задания, тем проще будет решение. Кажется, что звучит странно? Но действительно: при большом количестве известных величин можно пользоваться практически любыми формулами, а вот если предоставлена лишь пара чисел, могут потребоваться дополнительные размышления, придётся вспоминать и доказывать теоремы, приводить аргументы в пользу своей правоты…
К чему мы это? Да к тому, что обыкновенные дроби при всей своей громоздкости могут сильно упростить жизнь ученику, позволяя при перемножении и делении сокращать целые строки значений, а при расчёте суммы и разности выносить общие аргументы и, опять же, сокращать их.
Когда требуется осуществить совместные действия с обыкновенными и десятичными дробями, трансформации осуществляются в пользу первых: как вы переведете 3/17 в десятичный вид? Только с потерями информации, не иначе. А вот 0,1 можно представить как 1/10, а далее - как 17/170. И тогда два получившихся числа можно складывать или вычитать: 30/170 + 17/170 = 47/170.
Чем полезны десятичные дроби
Если действия с обыкновенными дробями осуществлять и сподручнее, то записывать все с их помощью крайне неудобно, десятичные здесь имеют существенное преимущество. Сравните: 1748/10000 и 0,1748. Это одно и то же значение, представленное в двух различных вариантах. Разумеется, второй способ проще!
Кроме того, десятичные дроби проще представить, поскольку все данные имеют общее основание, различающееся исключительно на порядки. Скажем, скидку в 30% мы легко осознаем и даже оценим как значительную. А сразу ли вы поймете, что больше - 30% или 137/379? Таким образом, десятичные дроби обеспечивают стандартизацию расчётов.
В старших классах ученики решают квадратные уравнения. Выполнять действия с обыкновенными дробями здесь уже крайне проблематично, поскольку формула для расчёта значений переменной содержит квадратный корень из суммы. При наличии дроби, не сводимой к десятичной, решение усложняется настолько, что рассчитать точный ответ без калькулятора становится практически невозможно.
Итак, каждый способ представления дробей имеет свои преимущества в соответствующем контексте.
Формы записи
Существует два способа записи действий с обыкновенными дробями: через горизонтальную черту, в два «яруса», и через наклонную черту (она же - «слэш») - в строку. Когда ученик пишет в тетради, первый вариант обычно удобнее, а потому и более распространен. Распределение рядом цифр по клеточкам способствует развитию внимательности при расчётах и проведении преобразований. При записи в строку можно по невнимательности перепутать порядок действий, потерять какие-либо данные - то есть, ошибиться.
Достаточно часто в наше время возникает необходимость напечатать числа на компьютере. Разделять дроби традиционной горизонтальной чертой можно, используя функцию в программе «Майкрософт Ворд» 2010 и более позднего года выпуска. Дело в том, что в этих версиях софта есть опция под названием «формула». Она выводит на экран прямоугольное трансформируемое поле, в рамках которого можно комбинировать любые математические символы, составлять и двух-, и «четырехэтажные» дроби. В знаменателе и числителе можно пользоваться скобками, знаками операций. В результате вы сможете записать любые совместные действия с обыкновенными и десятичными дробями в традиционной форме, т. е. так, как это учат делать в школе.
Если же вы будете пользоваться стандартным текстовым редактором «Блокнот», то все дробные выражения нужно будет писать через наклонную черту. Другого способа здесь, к сожалению, не предусмотрено.
Заключение
Вот мы и рассмотрели все основные действия с обыкновенными дробями, которых, оказывается, не так уж и много.
Если поначалу может казаться, что это сложный раздел математики, то это только временное впечатление - помните, когда-то вы так думали про таблицу умножения, а ещё раньше - про обычные прописи и счёт от одного до десяти.
Важно понимать, что дроби используются в повседневной жизни повсюду. Вы будете иметь дело с деньгами и инженерными расчётами, информационными технологиями и музыкальной грамотой, и везде - везде! - дробные числа будут фигурировать. Поэтому не поленитесь и изучите эту тему хорошенько - тем более не такая уж она и сложная.
1º. Натуральные числа - это числа, употребляемые при счете. Множество всех натуральных чисел обозначают N, т.е. N = (1, 2, 3, …).
Дробью называется число, состоящее из нескольких долей единицы. Обыкновенной дробью называется число вида , где натуральное число n показывает, на сколько равных частей разделена единица, а натуральное число m показывает, сколько таких равных частей взято. Числа m и n называют соответственно числителем и знаменателем дроби.
Если числитель меньше знаменателя, то обыкновенная дробь называется правильной ; если числитель равен знаменателю или больше него, то дробь называется неправильной . Число, состоящее из целой и дробной частей, называется смешанным числом .
Например, - правильные обыкновенные дроби, - неправильные обыкновенные дроби, 1 - смешанное число.
2º. При выполнении действий над обыкновенными дробями следует помнить следующие правила:
1) Основное свойство дроби . Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной.
Например, а) ; б) 
.
Деление числителя и знаменателя дроби на их общий делитель, отличный от единицы, называется сокращением дроби .
2) Чтобы смешанное число представить в виде неправильной дроби, нужно умножить его целую часть на знаменатель дробной части и к полученному произведению прибавить числитель дробной части, записать полученную сумму числителем дроби, а знаменатель оставить прежним.
Аналогично любое натуральное число можно записать в виде неправильной дроби с любым знаменателем.
Например, а) , так как ; б) 
и т.д.
3) Чтобы неправильную дробь записать в виде смешанного числа (т.е. из неправильной дроби выделить целую часть), нужно числитель разделить на знаменатель, частное от деления взять в качестве целой части, остаток - в качестве числителя, знаменатель оставить прежним.
Например, а) , так как 200: 7 = 28 (ост. 4);
б) , так как 20: 5 = 4 (ост. 0).
4) Чтобы привести дроби к наименьшему общему знаменателю, надо найти наименьшее общее кратное (НОК) знаменателей этих дробей (оно и будет их наименьшим общим знаменателем), разделить наименьший общий знаменатель на знаменатели данных дробей (т.е. найти дополнительные множители для дробей), умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Например, приведем дроби к наименьшему общему знаменателю:
630: 18 = 35, 630: 10 = 63, 630: 21 = 30.
Значит, 
; 
; 
.
5) Правила арифметических действий над обыкновенными дробями :
a) Сложение и вычитание дробей с одинаковыми знаменателями выполняется по правилу:
b) Сложение и вычитание дробей с разными знаменателями выполняется по правилу a), предварительно приведя дроби к наименьшему общему знаменателю.
c) При сложении и вычитании смешанных чисел можно обратить их в неправильные дроби, а затем выполнить действия по правилам a) и b),
Эта статья представляет собой общий взгляд на действия с дробями. Здесь мы сформулируем и обоснуем правила сложения, вычитания, умножения, деления и возведения в степень дробей общего вида A/B , где A и B некоторые числа, числовые выражения или выражения с переменными. По обыкновению материал будем снабжать поясняющими примерами с детальными описаниями решений.
Навигация по странице.
Правила выполнения действий с числовыми дробями общего вида
Давайте договоримся под числовыми дробями общего вида понимать дроби, в которых числитель и/или знаменатель могут быть представлены не только натуральными числами, но и другими числами или числовыми выражениями. Для наглядности приведем несколько примеров таких дробей: , 
.
Нам известны правила, по которым выполняются . По этим же правилам можно выполнять действия с дробями общего вида:
Обоснование правил
Для обоснования справедливости правил выполнения действий с числовыми дробями общего вида можно отталкиваться от следующих моментов:
- дробная черта - это по сути знак деления,
- деление на некоторое отличное от нуля число можно рассматривать как умножение на число, обратное делителю (этим сразу объясняется правило деления дробей),
- свойств действий с действительными числами ,
- и его обобщенном понимании ,
Они позволяют провести следующие преобразования, обосновывающие правила сложения, вычитания дробей с одинаковыми и разными знаменателями, а также правило умножения дробей:
Примеры
Приведем примеры выполнения действия с дробями общего вида по разученным в предыдущем пункте правилам. Сразу скажем, что обычно после проведения действий с дробями полученная дробь требует упрощения, причем процесс упрощения дроби часто сложнее, чем выполнение предшествующих действий. Мы не будем подробно останавливаться на упрощении дробей (соответствующие преобразования разобраны в статье преобразование дробей), чтобы не отвлекаться от интересующей нас темы.
Начнем с примеров сложения и вычитания числовых дробей с одинаковыми знаменателями. Для начала сложим дроби и . Очевидно, знаменатели равны. Согласно соответствующему правилу записываем дробь, числитель которой равен сумме числителей исходных дробей, а знаменатель оставляем прежним, имеем . Сложение выполнено, остается упростить полученную дробь: 
. Итак, 
.
Можно было решение вести по-другому: сначала осуществить переход к обыкновенным дробям, после чего провести сложение. При таком подходе имеем 
.
Теперь вычтем из дроби 
дробь 
. Знаменатели дробей равны, поэтому, действуем по правилу вычитания дробей с одинаковыми знаменателями:
Переходим к примерам сложения и вычитания дробей с разными знаменателями. Здесь главная сложность заключается в приведении дробей к общему знаменателю. Для дробей общего вида это довольно обширная тема, ее мы разберем детально в отдельной статье приведение дробей к общему знаменателю . Сейчас же ограничимся парой общих рекомендаций, так как в данный момент нас больше интересует техника выполнения действий с дробями.
Вообще, процесс схож с приведением к общему знаменателю обыкновенных дробей. То есть, знаменатели представляются в виде произведений, дальше берутся все множители из знаменателя первой дроби и к ним добавляются недостающие множители из знаменателя второй дроби.
Когда знаменатели складываемых или вычитаемых дробей не имеют общих множителей, то в качестве общего знаменателя логично взять их произведение. Приведем пример.
Допустим, нам нужно выполнить сложение дробей и 1/2
. Здесь в качестве общего знаменателя логично взять произведение знаменателей исходных дробей, то есть, . В этом случае дополнительным множителем для первой дроби будет 2
. После умножения на него числителя и знаменателя дробь примет вид . А для второй дроби дополнительным множителем является выражение . С его помощью дробь 1/2
приводится к виду . Остается сложить полученные дроби с одинаковыми знаменателями. Вот краткая запись всего решения:
В случае дробей общего вида речь уже не идет о наименьшем общем знаменателе, к которому обычно приводятся обыкновенные дроби. Хотя в этом вопросе все же желательно стремиться к некоторому минимализму. Этим мы хотим сказать, что не стоит в качестве общего знаменателя сразу брать произведение знаменателей исходных дробей. Например, совсем не обязательно брать общим знаменателем дробей и произведение 
. Здесь в качестве общего знаменателя можно взять .
Переходим к примерам умножения дробей общего вида. Умножим дроби и . Правило выполнения этого действия нам предписывает записать дробь, числитель которой есть произведение числителей исходных дробей, а знаменатель – произведение знаменателей. Имеем 
. Здесь, как и во многих других случаях при умножении дробей, можно сократить дробь: 
.
Правило деления дробей позволяет от деления переходить к умножению на обратную дробь. Здесь нужно помнить, что для того, чтобы получить дробь, обратную данной, нужно переставить местами числитель и знаменатель данной дроби. Вот пример перехода от деления числовых дробей общего вида к умножению: 
. Остается выполнить умножение и упростить полученную в результате дробь (при необходимости смотрите преобразование иррациональных выражений):
Завершая информацию этого пункта, напомним, что любое число или числовое выражение можно представить в виде дроби со знаменателем 1
, поэтому, сложение, вычитание, умножение и деление числа и дроби можно рассматривать как выполнение соответствующего действия с дробями, одна из которых имеет единицу в знаменателе. Например, заменив в выражении 
корень из трех дробью , мы от умножения дроби на число перейдем к умножению двух дробей: 
.
Выполнение действий с дробями, содержащими переменные
Правила из первой части текущей статьи применяются и для выполнения действий с дробями, которые содержат переменные. Обоснуем первое из них – правило сложения и вычитания дробей с одинаковыми знаменателями, остальные доказываются абсолютно аналогично.
Докажем, что для любых выражений A
, C
и D
(D
тождественно не равно нулю) имеет место равенство 
на его области допустимых значений переменных.
Возьмем некоторый набор переменных из ОДЗ. Пусть при этих значениях переменных выражения A
, C
и D
принимают значения a 0
, c 0
и d 0
. Тогда подстановка значений переменных из выбранного набора в выражение обращает его в сумму (разность) числовых дробей с одинаковыми знаменателями вида , которая по правилу сложения (вычитания) числовых дробей с одинаковыми знаменателями равна . Но подстановка значений переменных из выбранного набора в выражение обращает его в ту же дробь . Это означает, что для выбранного набора значений переменных из ОДЗ значения выражений и равны. Понятно, что значения указанных выражений будут равны и для любого другого набора значений переменных из ОДЗ, а это означает, что выражения и тождественно равны, то есть, справедливо доказываемое равенство .
Примеры сложения и вычитания дробей с переменными
Когда знаменатели складываемых или вычитаемых дробей одинаковые, то все довольно просто – складываются или вычитаются числители, а знаменатель остается прежним. Понятно, что полученная после этого дробь при надобности и возможности упрощается.
Заметим, что иногда знаменатели дробей отличаются лишь с первого взгляда, но по факту являются тождественно равными выражениями, как например, 
и , или и . А иногда достаточно упростить исходные дроби, чтобы «проявились» их одинаковые знаменатели.
Пример.
, б) 
, в) 
.
Решение.
а) Нам нужно выполнить вычитание дробей с одинаковыми знаменателями. Согласно соответствующему правилу знаменатель оставляем прежним и вычитаем числители, имеем 
. Действие проведено. Но еще можно раскрыть скобки в числителе и привести подобные слагаемые : 
.
б) Очевидно, знаменатели складываемых дробей одинаковые. Поэтому, складываем числители, а знаменатель оставляем прежним: . Сложение выполнено. Но несложно заметить, что полученную дробь можно сократить. Действительно, числитель полученной дроби можно свернуть по формуле квадрат суммы как (lgx+2) 2
(смотрите формулы сокращенного умножения), таким образом, имеют место следующие преобразования: 
.
в) Дроби в сумме имеют разные знаменатели. Но, преобразовав одну из дробей, можно перейти к сложению дробей с одинаковыми знаменателями. Покажем два варианта решения.
Первый способ. Знаменатель первой дроби можно разложить на множители, воспользовавшись формулой разность квадратов, после чего сократить эту дробь: 
. Таким образом, . Еще не помешает освободиться от иррациональности в знаменателе дроби: 
.
Второй способ. Умножение числителя и знаменателя второй дроби на (это выражение не обращается в нуль ни при каких значениях переменной x
из ОДЗ для исходного выражения) позволяет достичь сразу двух целей: освободиться от иррациональности и перейти к сложению дробей с одинаковыми знаменателями. Имеем
Ответ:
а) 
, б) 
, в) 
.
Последний пример подвел нас к вопросу приведения дробей к общему знаменателю. Там мы почти случайно пришли к одинаковым знаменателям, упрощая одну из складываемых дробей. Но в большинстве случаев при сложении и вычитании дробей с разными знаменателями приходится целенаправленно приводить дроби к общему знаменателю. Для этого обычно знаменатели дробей представляются в виде произведений, берутся все множители из знаменателя первой дроби и к ним добавляются недостающие множители из знаменателя второй дроби.
Пример.
Выполнить действия с дробями: а) 
, б) , в) 
.
Решение.
а) Здесь нет надобности что-либо делать со знаменателями дробей. В качестве общего знаменателя берем произведение 
. В этом случае дополнительным множителем для первой дроби выступает выражение , а для второй дроби – число 3
. Эти дополнительные множители приводят дроби к общему знаменателю, что в дальнейшем позволяет выполнить нужное нам действие, имеем
б) В этом примере знаменатели уже представлены в виде произведений, и никаких дополнительных преобразований не требуют. Очевидно, множители в знаменателях отличаются лишь показателями степеней, поэтому, в качестве общего знаменателя берем произведение множителей с наибольшими показателями, то есть, 
. Тогда дополнительным множителем для первой дроби будет x 4
, а для второй – ln(x+1)
. Теперь мы готовы выполнить вычитание дробей:
в) А в данном случае для начала поработаем со знаменателями дробей. Формулы разность квадратов и квадрат суммы позволяют от исходной суммы перейти к выражению 
. Теперь понятно, что эти дроби можно привести к общему знаменателю 
. При таком подходе решение будет иметь следующий вид:
Ответ:
а)
б)
в)
Примеры умножения дробей с переменными
Умножение дробей дает дробь, числитель которой есть произведение числителей исходных дробей, а знаменатель – произведение знаменателей. Здесь, как видите, все привычно и просто, и можно лишь добавить, что полученная в результате выполнения этого действия дробь часто оказывается сократимой. В этих случаях ее сокращают, если, конечно, это необходимо и оправданно.